hallo zusammen
Ich wollte eine post hoc Poweranalyse machen für mein Modell einer multiplen logistischen Regression.
Habe versucht zu verstehen was ich im GPower jeweils eintragen muss.
Kann mir jemand helfen was ich bei:
Pr (Y=1|X=1) H0
Pr (Y=1|X=1) H0
eintragen muss bzw. wie ich diese Wahrscheinlichkeiten herausfinden kann? Kann ich dies aus den Regressionskoeffizienten berechnen?
Vielen Dank für die Hilfe schon im Voraus und liebe Grüsse
G*Power Post Hoc Poweranalyse multiple logistische Regressio
Thema bewerten: 




 • 6 Beiträge
• Seite 1 von 1
• 6 Beiträge
• Seite 1 von 1
- lisa23
- Grünschnabel

- Beiträge: 9
- Registriert: Fr 22. Apr 2022, 14:28
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: G*Power Post Hoc Poweranalyse multiple logistische Regre
Hallo Lisa,
Vielleicht hilft Dir dieses Video? https://youtu.be/WJJCcvH61tQ
Wenn gar nichts anderes hilft, kann man auch das Handbuch von G* Power lesen. Logistische Regression ab S. 70, erläuterndes Beispiel auf Seite 71, Übergang zu mehreren Prädiktoren/ Kovariaten auf Seite 72: https://www.psychologie.hhu.de/fileadmi ... Manual.pdf
Erstmal ist das falsch abgeschrieben und das wirft die Frage auf, ob Du mit dieser Notation vertraut bist. Verstehst Du, was Du da geschrieben hast? Ist das oder etwas anders der Kern des Problems?
LG, Bernhard
Vielleicht hilft Dir dieses Video? https://youtu.be/WJJCcvH61tQ
Wenn gar nichts anderes hilft, kann man auch das Handbuch von G* Power lesen. Logistische Regression ab S. 70, erläuterndes Beispiel auf Seite 71, Übergang zu mehreren Prädiktoren/ Kovariaten auf Seite 72: https://www.psychologie.hhu.de/fileadmi ... Manual.pdf
lisa23 hat geschrieben:Pr (Y=1|X=1) H0
Pr (Y=1|X=1) H0
Erstmal ist das falsch abgeschrieben und das wirft die Frage auf, ob Du mit dieser Notation vertraut bist. Verstehst Du, was Du da geschrieben hast? Ist das oder etwas anders der Kern des Problems?
LG, Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5967
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: G*Power Post Hoc Poweranalyse multiple logistische Regre
Hallo Bernhard
Vielen Dank schon für deine Tipps und die schnelle Antwort.
Das Video und das Manual habe ich mir auch schon zuvor angeschaut.
Im Manual konnte ich folgendes finden.
Let p1 denote the probability of an event under H0, that is exp(β0) = p1/(1 − p1), and p2 the probability of an event under H1 at X = 1, that is exp(β0 + β1) = p2/(1 − p2).
Given the probability p1 (input field Pr(Y=1|X=1) H0) the effect size is specified either directly by p2 (input field) Pr(Y=1|X=1) H1) or optionally by the odds ratio (OR) (input field Odds ratio).
Die einzige Möglichkeit um jetzt an p1 zu kommen wäre ja die Gleichung zu lösen. Habe ich gemacht für B0 und B1 (aus meinem Regressionsmodell) ergibt aber nicht wirklich ein sinnvolles Ergebnis. Vielleicht steh ich auch grad komplett auf dem Schlauch
 Bin sehr dankbar um Hilfe dabei.
Bin sehr dankbar um Hilfe dabei.
Tatsächlich ist mir beim Abschreiben ein Fehler unterlaufen. Ich verstehe die Notation, das ist nicht das Problem.
Lieber Gruss
Lisa
Vielen Dank schon für deine Tipps und die schnelle Antwort.
Das Video und das Manual habe ich mir auch schon zuvor angeschaut.
Im Manual konnte ich folgendes finden.
Let p1 denote the probability of an event under H0, that is exp(β0) = p1/(1 − p1), and p2 the probability of an event under H1 at X = 1, that is exp(β0 + β1) = p2/(1 − p2).
Given the probability p1 (input field Pr(Y=1|X=1) H0) the effect size is specified either directly by p2 (input field) Pr(Y=1|X=1) H1) or optionally by the odds ratio (OR) (input field Odds ratio).
Die einzige Möglichkeit um jetzt an p1 zu kommen wäre ja die Gleichung zu lösen. Habe ich gemacht für B0 und B1 (aus meinem Regressionsmodell) ergibt aber nicht wirklich ein sinnvolles Ergebnis. Vielleicht steh ich auch grad komplett auf dem Schlauch
Tatsächlich ist mir beim Abschreiben ein Fehler unterlaufen. Ich verstehe die Notation, das ist nicht das Problem.
Lieber Gruss
Lisa
- lisa23
- Grünschnabel

- Beiträge: 9
- Registriert: Fr 22. Apr 2022, 14:28
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: G*Power Post Hoc Poweranalyse multiple logistische Regre
Hallo Lisa,
Sorry, das Publikum hier ist sehr gemischt und nicht immer geht aus den Fragen hervor, wo der Knoten sitzt.
Ich selbst habe G*Power nicht installiert. Ich entnehme dem Manual auf Seite 3, dass man da manchmal zwischen a priori und post hoc umschalten kann. Ich nehme mal an, das ist bei der logistischen Regression nicht der Fall?
An der Stelle verstehe ich nicht, warum Du p1 brauchst. Wäre es nicht viel einfacher, den Weg über die odds ratio zu nehmen, wenn Du die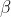 aus Deiner Regression post hoc doch schon hast?
aus Deiner Regression post hoc doch schon hast?
LG,
Bernhard
lisa23 hat geschrieben:Ich verstehe die Notation, das ist nicht das Problem.
Sorry, das Publikum hier ist sehr gemischt und nicht immer geht aus den Fragen hervor, wo der Knoten sitzt.
Ich selbst habe G*Power nicht installiert. Ich entnehme dem Manual auf Seite 3, dass man da manchmal zwischen a priori und post hoc umschalten kann. Ich nehme mal an, das ist bei der logistischen Regression nicht der Fall?
Let p1 denote the probability of an event under H0, that is exp(β0) = p1/(1 − p1), and p2 the probability of an event under H1 at X = 1, that is exp(β0 + β1) = p2/(1 − p2).
Given the probability p1 (input field Pr(Y=1|X=1) H0) the effect size is specified either directly by p2 (input field) Pr(Y=1|X=1) H1) or optionally by the odds ratio (OR) (input field Odds ratio).
Die einzige Möglichkeit um jetzt an p1 zu kommen wäre ja die Gleichung zu lösen.
An der Stelle verstehe ich nicht, warum Du p1 brauchst. Wäre es nicht viel einfacher, den Weg über die odds ratio zu nehmen, wenn Du die
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5967
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: G*Power Post Hoc Poweranalyse multiple logistische Regre
Hallo Bernhard
Vielen Dank für deine Antwort.
Kein Problem, versteh schon was du meinst. Und manchmal sitzt ja auch irgendwo der Knoten, wo man nie gedacht hätte
Tatsächlich kann man für die logistische Regression auch post hoc die Stichprobengrösse berechnen.
Das mit den Odds ist ein guter Punkt - bin auch davon ausgegangen, dass ich nur das benötige. G*Power benötigt jedoch folgende Angaben wenn man mit den Odds die Stichprobengrösse post hoc berechnen will.
tails = two
Odds Ratio = (habe ich aus meinen Daten)
Pr(Y=1|X=1) H0 = (fehlt mir)
alpha = 0.05
Stichprobengrösse = (habe ich aus meinen Daten)
R2 = (habe ich aus meinen Daten)
--> aus diesem Grund habe ich nach einer Möglichkeit gesucht, um nach p1 aufzulösen bzw. diese Wahrscheinlichkeit zu berechnen. Ich habe das Gefühl die Lösung ist nicht so weit weg haha aber ich komme auf kein gescheites Ergebnis.
Lieber Gruss
Lisa
Vielen Dank für deine Antwort.
Kein Problem, versteh schon was du meinst. Und manchmal sitzt ja auch irgendwo der Knoten, wo man nie gedacht hätte
Tatsächlich kann man für die logistische Regression auch post hoc die Stichprobengrösse berechnen.
Das mit den Odds ist ein guter Punkt - bin auch davon ausgegangen, dass ich nur das benötige. G*Power benötigt jedoch folgende Angaben wenn man mit den Odds die Stichprobengrösse post hoc berechnen will.
tails = two
Odds Ratio = (habe ich aus meinen Daten)
Pr(Y=1|X=1) H0 = (fehlt mir)
alpha = 0.05
Stichprobengrösse = (habe ich aus meinen Daten)
R2 = (habe ich aus meinen Daten)
--> aus diesem Grund habe ich nach einer Möglichkeit gesucht, um nach p1 aufzulösen bzw. diese Wahrscheinlichkeit zu berechnen. Ich habe das Gefühl die Lösung ist nicht so weit weg haha aber ich komme auf kein gescheites Ergebnis.
Lieber Gruss
Lisa
- lisa23
- Grünschnabel

- Beiträge: 9
- Registriert: Fr 22. Apr 2022, 14:28
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: G*Power Post Hoc Poweranalyse multiple logistische Regre
Ich wollte eine post hoc Poweranalyse machen für mein Modell einer multiplen logistischen Regression.
Warum bzw. zu welchem Zweck? Ich habe noch nie eine seriöse und kompetente Empfehlung dafür gesehen,
dementsprechend gibt es keine Veröffentlichungen, in denen das präsentiert wird (AFAIK).
Mit freundlichen Grüßen
PonderStibbons
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11389
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2510 mal in 2494 Posts
Thema bewerten: 




 • 6 Beiträge
• Seite 1 von 1
• 6 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 1 Gast


