Da die Frage nach der Interpretation von Interaktionen (auch: Moderatoreffekte) in linearen Regressionsmodellen eine FAQ zu sein scheint, hier ein Versuch, die allgemeine Vorgehensweise zu erläutern. Die Interpretation einer linearen Regressionsanalyse ohne Interaktionen sollte bereits bekannt sein.
Gegeben sei das lineare Regressionsmodell
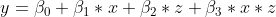
Der Einfachheit halber verzichte ich auf explizite Subskripte. Alternativ stelle man sich
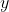
,

und

als Vektoren vor.
Die Interpretation der Koeffizienten lässt sich an diesem Modell eigentlich direkt ablesen. Beginnen wir vorn, mit der Konstanten.
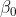
gibt den erwarteten Wert (Durchschnitt) in
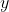
an, falls

und

den Wert 0 annehmen. Wieso? Setzen wir ein:
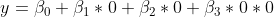
Da ein Produkt den Wert Null annimmt, sobald einer der Faktoren Null ist, fallen bis auf
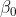
alle Terme aus der Gleichung. Das wäre nicht der Fall, wenn

und/oder

nicht Null wären. Bis zu dieser Stelle gleicht die Interpretation einem Regressionsmodell ohne Interaktion.
Wie lassen sich die anderen Koeffizienten interpretieren? Nun,
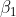
gibt an, um wie viele Einheiten sich
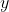
durchschnittlich mit der Änderung einer Einheit in

verändert,
falls  den Wert Null annimmt
den Wert Null annimmt. Da

nicht nur einmal im Modell steckt, sondern als Teil der Interaktion (Produktterm

) zweimal, kann
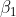
nicht (mehr) als einfacher Haupteffekt (oder schlicht: Effekt) von

interpretiert werden. Vielmehr wird
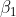
als
konditionaler Haupteffekt von

bezeichnet.
Es ist auch klar, dass

nicht mehr
einen (konstanten) Effekt hat. Wir haben die Interaktion ja gerade deshalb im Modell spezifiziert, weil wir vermuten, dass der Effekt von

konditional, also abhängig von der Ausprägung der Variablen

ist.
Wieso ist
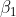
der Effekt von

an der Stelle
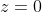
? Naja, setzen wir wieder ein:
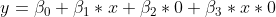
Im Falle
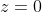
fällt also der komplette Produktterm aus der Gleichung. Die Änderung in
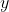
, die bei einer Änderung in

zu erwarten ist, lässt sich in diesem Fall einfach an
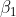
ablesen.
Und was ist nun der Effekt von

, wenn

nicht Null ist?
Aus den vorherigen Überlegungen zur obigen Gleichung wird deutlich, dass für jeden Wert
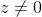
der letzte Term
nicht aus der Gleichung fällt (es sei denn
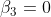
). Da dieser Term aber neben

eben auch

beinhaltet, verändert sich
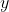
nun mit einer (Einheit) Änderung in

, um
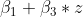
. Der (globale) Effekt von

auf
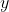
ist also
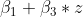
.
Es verteht sich von selbst, dass die Interpretation des Effekts von

genau analog verläuft. Interaktionen sind statistisch/mathematisch niemals nur in einer Richtung zu interpretieren, auch wenn theoretisch/ökonometrisch nur eine Richtung interessant und/oder sinnvoll ist.
Die Interpretation der t-Tets der Koeffizienten folgt den gleichen Überlegungen. Zur Interpretation möchte ich mich an dieser Stelle einfach selbst zitieren.
Die Nullhypothesen, die R (und andere Statistiksoftware) automatisch testet, lauten:
H0: der
Koeffizient 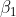
ist nicht von Null verschieden.
H0: der
Koeffizient 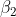
ist nicht von Null verschieden.
H0: der
Koeffizient 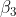
ist nicht von Null verschieden.
Was wir aber interpretieren möchten, sind meist Hypothesen der Art
H0: der
Effekt von

ist nicht von Null verschieden.
H0: der
Effekt von

ist nicht von Null verschieden.
H0: der
Effekt von

auf den Effekt von

(und umgekehrt) ist nicht von Null verschieden.
Nun stellt sich die Frage, was der
Effekt ist.
Diese Frage haben wir bereits beantwortet, es gilt jetzt nur noch sich dieser Antwort bei der Interpretation der Signifikanztests bewusst zu sein.
Ein insignifikanter Koeffizient
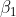
bedeutet
nicht, dass

keinen statistisch signifikanten Effekt hat. Es bedeutet schlicht, dass der Effekt von

auf
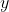 an der Stelle
an der Stelle 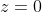
statistisch nicht signifikant von Null verschieden ist.
Ein insignifikanter Koeffizient
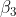
bedeutet, dass es keine statistisch signifikante Wechselwirkung von

und

gibt.
Nach der Lektüre dieses Beitrags sollte die Interpretation von Interaktionen zwischen zwei metrischen Variablen, die Interaktionen zwischen binären Variablen und die Interaktion zwischen einer metrischen und einer binären Variablen erleichtert sein.
Interaktionen mit kategorialen Variablen, mit
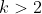
Ausprägungen folgen (selbstverständlich) der gleichen Logik. Sie sind zugegeben etwas schwieriger zu interpretieren, aber auch dafür dürfte der Beitrag einen gute Grundlage sein.
Eine lange, hoffentlich interessante Diskussion eines Anwendungsbeispiels einer Interaktion zweier binärer Variablen findet sich hier:
regressionanalyse-f11/interaktionseffekt-t1190.htmlStata is an invented word, not an acronym, and should not appear with all letters capitalized: please write “Stata”, not “STATA”.
ist nicht von Null verschieden.
ist nicht von Null verschieden.
ist nicht von Null verschieden.
ist nicht von Null verschieden.
ist nicht von Null verschieden.
auf den Effekt von
(und umgekehrt) ist nicht von Null verschieden.




