STATISTIK-FORUM.de

[Malinko]

Hallo ihr Lieben,

ich bin neu hier und würde mich über eure Hilfe freuen! Ich schreibe gerade meine Masterarbeit über das Thema „Neuproduktbedarfsprognose“ und suche ein Verfahren, das mir bei der folgenden Idee weiterhilft:
Es gibt ein Produkt, dessen Modelle jeweils verschiedene Merkmale und Ausprägungen besitzen (leider alle qualitativ, werden aber in eine Rangskala überführt). Zu jeder Produktvariante, das heißt verschiedenste Kombinationen der Ausprägungen, habe ich Verkaufszahlen in Stück.

Das Ziel ist dann, wie unten in dem Bild mit Hilfe von Linearkombinationen die zu erwartende Verkaufszahl für ein neues Produkt zu erhalten.

Ihr seht hier (Link) als Beispiel die zwei Merkmale Farbe und Glanz (es gibt insgesamt etwa 15) und dazu allein für die jeweilige Ausprägung die Verkaufszahlen in Stück. Ich suche nun eine Methode, mit der man die Gewichtung der Merkmale für die Kaufentscheidung errechnen kann. Also z.B. dass die Farbe 75% Einfluss auf die verkauften Stück hat und der Glanz 25%. Das müsste doch möglich sein, wenn ich zu den verschiedensten Kombinationen Daten habe?

https://www.dropbox.com/s/qs91w5y0e2v1fba/bild.JPG

Über eure Hilfe würde ich mich sehr freuen!
Viele Grüße,
Malinko

[bele]

Hallo Malinko,

wie willst Du denn die Farbe in eine Rangskala bringen? Das klingt unwahrscheinlich. Auch ob ich etwas matt, leicht oder stark glänzend kaufe muss ja für die Kaufpräferenz keine Rangskala sein. Vielleicht mag ich immer leicht glänzend aber beide Extreme nicht? Ohne weitere Erklärung glaube ich nicht an die Rangskalen.

Stell Dir vor, Du beschreibst jedes Modell mit sog. Dummivariablen. Z. B. ist die Dummy-Variable immer Null, wenn das Modell nicht schwarz ist aber Eins, wenn es schwarz ist. Dasselbe mit und .

Wenn Du wirklich alle Kombinationen hast, dann berechnet Dir jedes beliebige Statistikprogramm Werte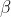 die folgende Gleichung annähern:


Aus diesen Betas kannst Du leicht ersehen, welchen Beitrag jede Farbe oder jeder Glanzgrad im linearen Modell auf die Verkaufszahlen hat. Der Suchbegriff dazu heißt "lineare Regression". Im Detail ist es schon etwas schwieriger und vielleicht ist es besser, Du wendest Dich an jemanden, der so etwas kann statt das jetzt für eine Frage alles selbst zu lernen.

LG,
Bernhard

[Malinko]

Hallo,

vielen Dank, das ist ein guter Ansatz, ich denke der wird mich schon mal voranbringen!

Die Idee mit der Rangskala war so, dass ich z.B. nur die Farbe betrachtet, nach den Verkaufszahlen schaue und dann die Farbe in Ränge bringe. Also 1. schwarz, weil meistverkauft, dahinter weiß weil zweithöchste Verkaufszahl usw. Kann man das so machen?

Ein Gedanke von mir war noch, die Faktorenanalyse anzuwenden und hier die Faktorladungen als Gewichtung zu nehmen. Zumal man da ja dann nur mit einem Faktor arbeiten dürfte. Aber ich weiß nicht, ob mein Gedanke da richtig ist.


Viele Grüße,
Malinko

[bele]

Ich frage mich dazu gerade noch, ob man dann zu jedem Modell eine solche Gleichung hat (also zu dem jeweiligen Modell mit der dazugehörigen Verkaufszahl), dann hätte man ja für jedes Modell einzeln die ß-Werte. Wie bringt man die dann alle wieder zusammen?

Wenn das vom statistischen Modell überhaupt so linear zusammen passt, dann kannst Du auch die Modelle mit Dummy-Variablen kodieren und so gemeinsame Betas erhalten. Am Schluss käme dann so etwas heraus wie:

Verkäufe(Luxusmodell,Rot,Leicht) = Verkäufe-Grundmodell - 40 VerkäufeWegenLuxusmodell + 101,3 VerkäufeWegenRot + 50,2 VerkäufeWegenLeicht

Nur wenn so eine Formel inhaltlich Sinn macht, solltest Du sie mit einer linearen Regression aufstellen.

Die Idee mit der Rangskala war so, dass ich z.B. nur die Farbe betrachtet, nach den Verkaufszahlen schaue und dann die Farbe in Ränge bringe. Also 1. schwarz, weil meistverkauft, dahinter weiß weil zweithöchste Verkaufszahl usw. Kann man das so machen?

Mir fällt gerade nicht ein, warum und wozu man das machen sollte. Bei welcher Operation würde es Dir helfen?

Ein Gedanke von mir war noch, die Faktorenanalyse anzuwenden und hier die Faktorladungen als Gewichtung zu nehmen. Zumal man da ja dann nur mit einem Faktor arbeiten dürfte.

Eine Faktorenanalyse machen, um sich vorher schon auf einen Faktor festzulegen, ist doch irgendwie eine Vergewaltigung des Verfahrens. Nach meinem Verständnis wäre eine Faktorenanalyse dazu da, Zusammenhänge zwischen den verschiedenen Produkteigenschaften zu untersuchen, aber andere im Forum haben sicher ein tiefer gehendes Verständnis der Möglichkeiten von Faktorenanalysen als ich. Vielleicht willst Du auch etwas anderes erreichen als ich denke.

LG,
Bernhard


Viele Grüße,
Malinko[/quote]

[Malinko]

Hallo,
vielen Dank für deine Antwort.
Die Kodierung der Modelle mit Dummies, um so gemeinsame ß zu erhalten, habe ich aber noch nicht verstanden, kannst du das nochmal genauer erklären?

Die Datenmatrix sähe in meinem Fall dann ja etwa so aus:


Also hätte ich dann für jedes Modell eine Funktion in der Art:


Mein Problem ist jetzt folgendes, das Ziel ist ja eine einzelne Funktion zu erreichen, die dann etwa so aussieht und mit der ich dann nach Einsetzen der Variablenausprägungen die Verkaufszahl erhalte:


Wie komme ich dahin?

Ganz einfach gedacht, müsste ich doch mit den einzelnen Modellfunktionen oben die unbekannten Variablen (ßx) berechnen können und brauche sie dann nur noch in die Zielfunktion einsetzen? Also einfach die multiple Regressionsgleichung der Datenmatrix berechnen lassen. Aber das klingt mir irgendwie zu leicht.
_______________

Die Rangsskala hatte ich mir überlegt, um aus den qualitativen metrische Daten zu machen, aber die Dummyvariante ist da besser!

Vielen lieben Dank für eure Antworten, die helfen mir wirklich sehr!
Malinko

[bele]

Jetzt muss ich nachfragen, weil ich es nicht richtig verstanden habe. Ist Modell 1 immer rot und Modell 2 immer schwarz oder gibt es alle Modelle in allen Farben. Ich war von letztem ausgegangen. Wenn es so wie oben abgebildet ist, brauchst Du die Modelle natürlich nicht als Dummies zu codieren.

Also hätte ich dann für jedes Modell eine Funktion in der Art:

Im Prinzip ja, außer dass da jetzt überall 700 Verkäufe eingetragen sind, Du aber bestimmt verschiedene Zahlen für jedes Modell gemeint hast.

Mein Problem ist jetzt folgendes, das Ziel ist ja eine einzelne Funktion zu erreichen, die dann etwa so aussieht und mit der ich dann nach Einsetzen der Variablenausprägungen die Verkaufszahl erhalte:

Du erhälst nicht die Verkaufszahl, sondern die vom statistischen Modell vorhergesagte Verkaufszahl. Die wird ein Stück weit neben der tatsächlichen Verkaufszahl liegen.

Wie komme ich dahin?

Indem Du die Zahlen in das Statistikprogramm Deiner Wahl eingibst und eine multiple lineare Regression durchführen lässt. (Wenn Du das beruflich brauchst, es also wirklich um was geht, wäre das die Stelle an der ich raten würde, sich Hilfe zu holen.)

Aber das klingt mir irgendwie zu leicht.

Keine Sorge, die Probleme kommen schon noch. Zum Beispiel bei der Frage, ob Du genug Daten hast, um das Modell zu spezifizieren. Oben willst Du mit den Daten von 5 Modellen 6 Betas berechnen. Das wird nicht klappen, weil das (statistische) Modell unterspezifiziert ist. Das nächste Problem wird die Frage sein, wie weit ein einfaches lineares Modell die Wirklichkeit des Käuferverhaltens widerspiegeln kann.

LG,
Bernhard

[Malinko]

Hallo,

noch eine Frage, die mir gerade aufgekommen ist:

Es geht um die multiple Regressionsanalyse. Wenn ich nun eine (unabhängige) Variabel dabei habe, bei der ich nicht für alle Modelle einen Wert habe, kann ich diese trotzdem miteinbringen oder verfälscht es das Ergebnis zu sehr? Zur besseren Erklärung: zu jedem Modell, das ich habe, möchte ich gerne einen Wirtschaftsindex (zum Zeitpunkt der Markteinführung) dazunehmen. Nun gibt es einen branchenspezifischen Index, der aber erst 2006 startet. Ich habe aber in meinen Daten auch Modelle, die älter sind und daher für diese keinen Wert für diesen branchenspezifischen Index.

Was denkt ihr?

Viele Grüße,
malinko