Hallo Zusammen,
ich möchte eine Frage zu meinem Versuchsaufbau bzw. zur Bestimmung einer Stichprobengröße loswerden. Würde mich über ein paar Anregungen freuen.
Ich stehe vor einem riesigen Sack von ca. 1000 kg Erbsen (die absolute Zahl an Erbsen kenne ich nicht, sondern kann diese nur Abschätzen). Mir wurde gesagt, dass auf eine Million Erbsen ca. 50-200 schlechte Erbsen dabei sind.
Wie groß muss ich meine Stichprobe machen, damit ich den Wert der schlechten Erbsen aus dem Sack statistisch auf +/- 10 ppm bestimmen kann?
Ich könnte mir ja mit einer Probe aus dem Erbsensack eine durchschnittliches Erbsengewicht errechnen. Die schlechten Erbsen sind im Verhältnis zu den guten Erbsen vernachlässigbar leicht und eh nur in sehr geringer Konzentration vorhanden. Aber die Gewichtsanteile helfen nur bei unterscheidlichen Erbsengewichten?
Danke für ein paar Anstöße!
Probengröße bei Sortiervorgang
Thema bewerten: 




 • 7 Beiträge
• Seite 1 von 1
• 7 Beiträge
• Seite 1 von 1
- 0skarina
- Grünschnabel

- Beiträge: 4
- Registriert: Mo 9. Dez 2019, 16:43
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Probengröße bei Sortiervorgang
Um mein Problem neu zu formulieren:
Der Erbsensack enthält 2 Mio. Erbsen. In dem Sack befinden sich auch eine unbekannte Zahl vergammelter Erbsen.
Wie kann ich in einem solchen Fall eine minimale Probengröße bestimmen, die ich aus dem Sack ziehen muss, mit der ich über Auszählen die Kontamination des Erbsensacks insgesamt zuverlässig (>95% Konfidenz) bestimmen kann?
Der Erbsensack enthält 2 Mio. Erbsen. In dem Sack befinden sich auch eine unbekannte Zahl vergammelter Erbsen.
Wie kann ich in einem solchen Fall eine minimale Probengröße bestimmen, die ich aus dem Sack ziehen muss, mit der ich über Auszählen die Kontamination des Erbsensacks insgesamt zuverlässig (>95% Konfidenz) bestimmen kann?
- 0skarina
- Grünschnabel

- Beiträge: 4
- Registriert: Mo 9. Dez 2019, 16:43
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Probengröße bei Sortiervorgang
Hallo Oskarina,
sagen wir, Du hast 1 Mio Erbsen und jede von denen hat immer das gleiche Risiko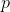 , eine schlechte Erbse zu sein. In Deinem Fall mag
, eine schlechte Erbse zu sein. In Deinem Fall mag 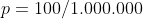 sein. Du ziehst nun
sein. Du ziehst nun  Erbsen und beobachtest darin
Erbsen und beobachtest darin  schlechte Erbsen. Dann folgt
schlechte Erbsen. Dann folgt  einer Binomialverteilung und "binomial" sollte Teil der Suchbegriffe sein, mit denen Du Dich dem Problem näherst.
einer Binomialverteilung und "binomial" sollte Teil der Suchbegriffe sein, mit denen Du Dich dem Problem näherst.
Ich benutze gerne das kostenlose Statistikprogramm R, das man sich von http://www.r-project.org herunterladen kann. Nehmen wir an, Du hast 100.000 Erbsen untersucht und darin 10 schlechte gefunden. Dann würde ich in R folgendes eingeben:
und R würde antworten:
Das bedeutet: Das 95%-Konfidenzintervall für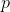 , also den wahren Anteil an schlechten Erbsen liegt nach dieser Beobachtung zwischen 0,000048 und 0,00018, d. h. zwischen 0,0048 % und 0,018%. Statt in Prozent kannst du das auch in ppm umrechnen. Du hast nun einerseits die Wahl, mit verschiedenen
, also den wahren Anteil an schlechten Erbsen liegt nach dieser Beobachtung zwischen 0,000048 und 0,00018, d. h. zwischen 0,0048 % und 0,018%. Statt in Prozent kannst du das auch in ppm umrechnen. Du hast nun einerseits die Wahl, mit verschiedenen  und
und  herumzuspielen bis Du zu dem Schluss kommst, dass bei einem bestimmen
herumzuspielen bis Du zu dem Schluss kommst, dass bei einem bestimmen  die Präzision der Bestimmung (die Weite des Konfidenzintervalls) ausreicht.
die Präzision der Bestimmung (die Weite des Konfidenzintervalls) ausreicht.
Alternativ beschäftigst Du Dich mit der Binomialverteilung und mit sog. Poweranalysen zur Fallzahlbestimmung. Dann umgehst Du den Bereich des "Herumprobierens", musst Dich aber mit mehr theoretischen Konzepten wie Poweranalyse, Effektstärkemaße etc. beschäftigen.
HTH,
Bernhard
sagen wir, Du hast 1 Mio Erbsen und jede von denen hat immer das gleiche Risiko
Ich benutze gerne das kostenlose Statistikprogramm R, das man sich von http://www.r-project.org herunterladen kann. Nehmen wir an, Du hast 100.000 Erbsen untersucht und darin 10 schlechte gefunden. Dann würde ich in R folgendes eingeben:
- Code: Alles auswählen
binom.test(x=10, n=100000)$conf.int
und R würde antworten:
- Code: Alles auswählen
[1] 0.0000479549 0.0001838958
Das bedeutet: Das 95%-Konfidenzintervall für
Alternativ beschäftigst Du Dich mit der Binomialverteilung und mit sog. Poweranalysen zur Fallzahlbestimmung. Dann umgehst Du den Bereich des "Herumprobierens", musst Dich aber mit mehr theoretischen Konzepten wie Poweranalyse, Effektstärkemaße etc. beschäftigen.
HTH,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5973
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1411 mal in 1397 Posts
Re: Probengröße bei Sortiervorgang
Hi,
- zur Vertiefung und Ergänzung zum Grundverständnis könnte die Hypergeometrische Verteilung eine Rolle spielen.
Gruß
S.
- zur Vertiefung und Ergänzung zum Grundverständnis könnte die Hypergeometrische Verteilung eine Rolle spielen.
Gruß
S.
- strukturmarionette
- Schlaflos in Seattle

- Beiträge: 4372
- Registriert: Fr 17. Jun 2011, 22:15
- Danke gegeben: 32
- Danke bekommen: 587 mal in 584 Posts
Re: Probengröße bei Sortiervorgang
Hallo bele, hallo strukturmarionette,
vielen Dank für eure Antworten. Ich habe mich tatsächlich eingelesen, um mich der Thematik (wieder) zu nähern.
Also, ich habe eine dichotome Grundgesamtheit und eine hypergeometrische Verteilung der Grundgesamtheit (ich lege nicht zurück).
Angenommen ich könnte aus Erfahrung sagen, dass es in dem Erbsensack zwischen 50 und 150 schlechte Erbsen pro 1 Mio. Erbsen gibt.
...und ich ziehe eine Stichprobe, dann wäre doch das zu erwartende arithmetische Mittel der Stichprobe X̅ = [0,00005 + 0,0002]/2= 0,000125...und damit als geschätzte Gesamtkontamination zu interpretieren. Oder?
Kann mir dieses Schätzintervall der Erbsenkontamination auch als Länge L meines Konfidenzintervalls dienen? D.h. L = 0,000125
Bei meiner Recherche bin ich darauf gestoßen, dass mir die Standardabweichung als Schätzer der Stichprobenvarianz dienen kann, über die Formel im Bildlink: https://ibb.co/rF571Yf
Die Stichprobengröße würde sich dann in Abhängigkeit der geschätzten Stichprobenvarianz, Länge des Konfidenzintervalls und z als das jeweilige Fraktil der Normalverteilung ergeben...
Ist der Ansatz aus eurer Sicht in Ordnung?
vielen Dank für eure Antworten. Ich habe mich tatsächlich eingelesen, um mich der Thematik (wieder) zu nähern.
Also, ich habe eine dichotome Grundgesamtheit und eine hypergeometrische Verteilung der Grundgesamtheit (ich lege nicht zurück).
Angenommen ich könnte aus Erfahrung sagen, dass es in dem Erbsensack zwischen 50 und 150 schlechte Erbsen pro 1 Mio. Erbsen gibt.
...und ich ziehe eine Stichprobe, dann wäre doch das zu erwartende arithmetische Mittel der Stichprobe X̅ = [0,00005 + 0,0002]/2= 0,000125...und damit als geschätzte Gesamtkontamination zu interpretieren. Oder?
Kann mir dieses Schätzintervall der Erbsenkontamination auch als Länge L meines Konfidenzintervalls dienen? D.h. L = 0,000125
Bei meiner Recherche bin ich darauf gestoßen, dass mir die Standardabweichung als Schätzer der Stichprobenvarianz dienen kann, über die Formel im Bildlink: https://ibb.co/rF571Yf
Die Stichprobengröße würde sich dann in Abhängigkeit der geschätzten Stichprobenvarianz, Länge des Konfidenzintervalls und z als das jeweilige Fraktil der Normalverteilung ergeben...
Ist der Ansatz aus eurer Sicht in Ordnung?
- 0skarina
- Grünschnabel

- Beiträge: 4
- Registriert: Mo 9. Dez 2019, 16:43
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Probengröße bei Sortiervorgang
bele hat geschrieben:Hallo Oskarina,
sagen wir, Du hast 1 Mio Erbsen und jede von denen hat immer das gleiche Risiko, eine schlechte Erbse zu sein. In Deinem Fall mag
sein. Du ziehst nun
Erbsen und beobachtest darin
schlechte Erbsen. Dann folgt
einer Binomialverteilung und "binomial" sollte Teil der Suchbegriffe sein, mit denen Du Dich dem Problem näherst.
Ich benutze gerne das kostenlose Statistikprogramm R, das man sich von http://www.r-project.org herunterladen kann. Nehmen wir an, Du hast 100.000 Erbsen untersucht und darin 10 schlechte gefunden. Dann würde ich in R folgendes eingeben:
- Code: Alles auswählen
binom.test(x=10, n=100000)$conf.int
und R würde antworten:
- Code: Alles auswählen
[1] 0.0000479549 0.0001838958
Das bedeutet: Das 95%-Konfidenzintervall für, also den wahren Anteil an schlechten Erbsen liegt nach dieser Beobachtung zwischen 0,000048 und 0,00018, d. h. zwischen 0,0048 % und 0,018%. Statt in Prozent kannst du das auch in ppm umrechnen. Du hast nun einerseits die Wahl, mit verschiedenen
und
herumzuspielen bis Du zu dem Schluss kommst, dass bei einem bestimmen
die Präzision der Bestimmung (die Weite des Konfidenzintervalls) ausreicht.
Alternativ beschäftigst Du Dich mit der Binomialverteilung und mit sog. Poweranalysen zur Fallzahlbestimmung. Dann umgehst Du den Bereich des "Herumprobierens", musst Dich aber mit mehr theoretischen Konzepten wie Poweranalyse, Effektstärkemaße etc. beschäftigen.
HTH,
Bernhard
Hi Bernhard,
ich verstehe nicht, warum R eine Binomialverteilung nutzt. Sollte das nciht die hypergeometrische Verteilung sein?
Ich ziehe ja auf ein Mal, ohne Zurücklegen eine Hand voll Erbsen.
- 0skarina
- Grünschnabel

- Beiträge: 4
- Registriert: Mo 9. Dez 2019, 16:43
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Probengröße bei Sortiervorgang
0skarina hat geschrieben:ich verstehe nicht, warum R eine Binomialverteilung nutzt. Sollte das nciht die hypergeometrische Verteilung sein?
Hallo 0skarina,
das ist nicht der Fehler von R, sondern mein Fehler. Wenn Du Deinem Erbsensack eine Erbse entnimmst, ändert das an den Wahrscheinlichkeiten fast nichts. Wenn Du natürlich einen erheblichen Anteil der 1 Mio. Erbsen entnimmst hast Du Recht, dann kann man irgendwann die Binomialverteilung nicht mehr als Näherung der hypergeometrischen Verteilung verwenden.
Während es für R natürlich auch viele Funktionen zur Beschreibung hypergeometrischen Verteilungen gibt war ich noch nie in der Situation, wo zwischen beiden ein quantitativ relevanter Unterschied bestand und ich mich näher damit hätte beschäftigen müssen. Daher bin ich hier wohl der falsche Ratgeber.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5973
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1411 mal in 1397 Posts
Thema bewerten: 




 • 7 Beiträge
• Seite 1 von 1
• 7 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 1 Gast


